GPT-5 Pro独立做数学研究！读论文后给出更精确边界，OpenAI总裁：这是生命迹象

66 0 0

文章摘要

OpenAI研究人员喂给GPT – 5 Pro一篇关于凸优化问题的论文，模型读完后针对边界问题给出比原文更精确的阈值和相应证明，引发全网热议。不过研究人员未将其成果发表成论文，因论文更新版本给出新边界反超了GPT – 5 Pro，但GPT – 5 Pro证明思路不同，具备独立探索能力，OpenAI总裁称此为“生命迹象”。

这篇论文研究凸优化问题，聚焦“当使用梯度下降算法优化光滑凸函数时，其产生的优化曲线是否是凸的”。论文结论指出优化曲线凸性关键取决于步长选择：当步长η ∈ (0, 1/L]时，优化曲线保证是凸的；当步长η ∈ (1.75/L, 2/L)时，优化曲线可能非凸；对于整个收敛区间η ∈ (0, 2/L]，梯度范数序列||∇f(x_n)||单调递减；对于凸且二阶连续可导函数及凸L – 光滑函数，梯度流的优化曲线总是凸的；对于连续时间的梯度流，优化曲线也总是凸的。论文证明凸性保证区间核心是证明序列{f(x__n) – f[(x__(n + 1)]}非递增，引入辅助函数g_k(t)转化为连续函数积分证明；非凸可能区间则构造分段函数作为反例。

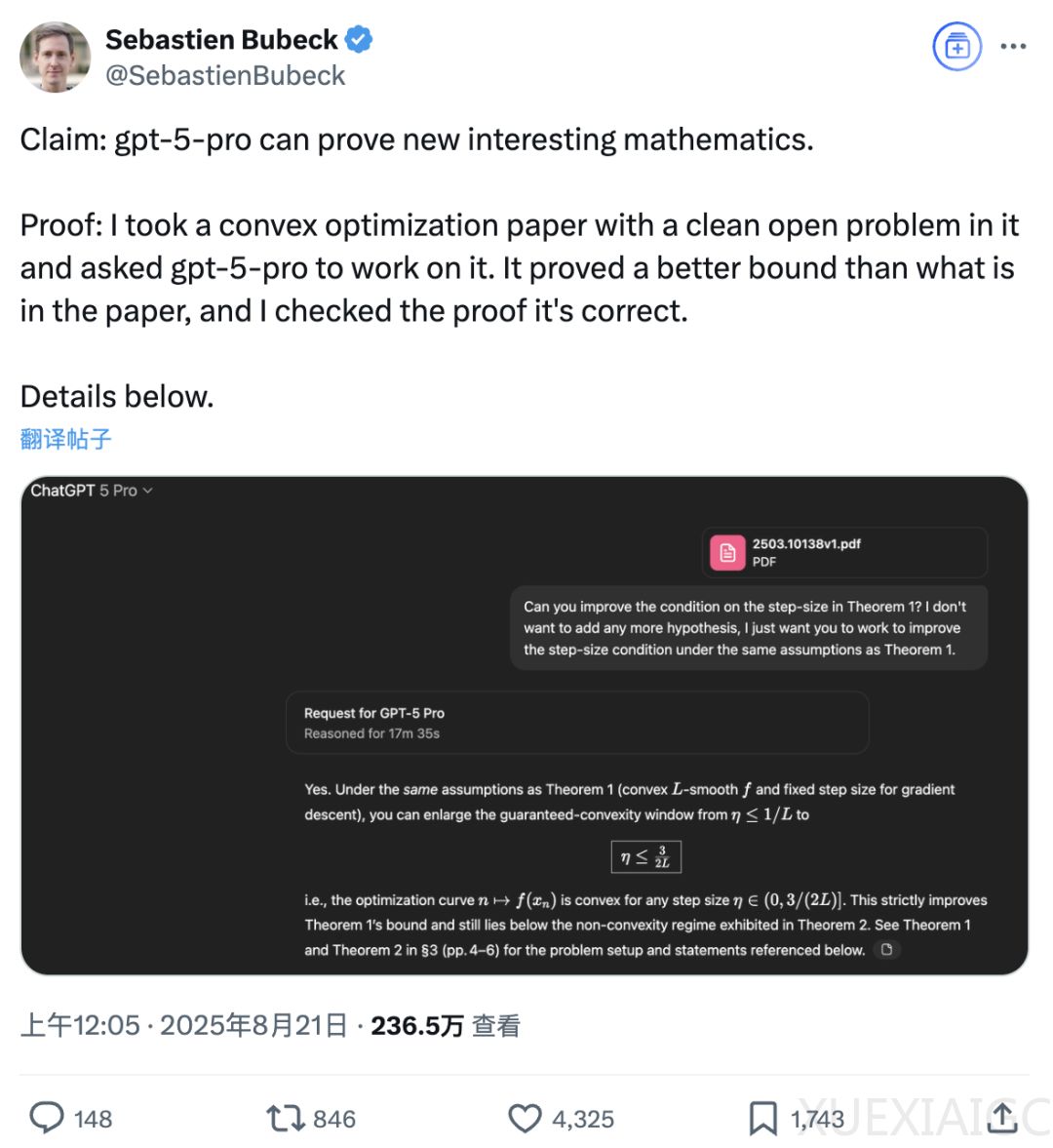
在论文第一版中，(1/L, 1.75/L]范围内未有定论。GPT – 5 Pro通过更精细不等式技巧，17分半将1/L边界移到1.5/L，其核心思路是将优化曲线凸性问题转化为证明函数值下降量递减，运用Bregman散度不等式和标准的共强制性不等式细化凸性条件。之后论文原作者更新论文，证明1.75/L是精确界限，闭合之前未探索区间。虽GPT – 5 Pro证明被人类反超，但思路和过程与新版论文不同，表明其确实具备自主发现并证明数学规律的能力。