大模型的第一性原理：（二）信号处理篇

AIGC动态2小时前发布 almosthuman2014

58 0 0

文章摘要

大模型的输入是Token的语义嵌入（语义向量），本质是将自然语言处理问题转换为信号处理问题。向量化在这一过程中至关重要，它与信号处理和信息论存在深刻联系。尽管语法和逻辑在人类语言中占据关键地位，但大模型仅从纯概率角度建模自然语言。Token的向量化使得定义内积成为可能，从而大幅降低计算复杂度，并进一步衍生出距离、微分和低维流形等可数值计算的概念，为神经网络训练奠定基础。研究表明，神经网络之所以能完成分类任务，正是因为同类事物在高维参数空间中会内聚成低维流形。

语义向量化的核心思想是用内积表示Token层面的语义相关性。语义向量空间被定义为M维单位球面，其中每个Token对应球面上的一个点。值得注意的是，单个向量本身并无语义，其与其他所有向量的内积（相对关系）才代表语义。这与传统信源编码有本质区别，后者是对单个符号的压缩，而语义向量压缩需保持相对关系不变。Gromov-Wasserstein距离被引入以衡量语义空间降维带来的精度损失或不同语言间的语义差异，该数学工具由几何学家Mikhael Gromov提出，拓展了最优传输理论的应用范围。

语义压缩问题涉及将高维语义空间降至合适维度。Johnson-Lindenstrauss（JL）引理证明，通过线性变换可在降低维度的同时控制内积误差。若结合语义向量的稀疏性，还可利用压缩感知理论强化JL引理，开发更高效的压缩算法。最优语义向量化应围绕预测下一个Token的目标展开，其数学形式可表述为条件互信息最大化问题。Google DeepMind团队提出的Contrastive Predictive Coding（CPC）算法通过最小化InfoNCE损失函数逼近这一目标，但并非理论最优解。定向信息概念的引入为优化语义编码器提供了新思路，但其计算复杂度较高。

Transformer本质上是一种非线性时变向量自回归时间序列模型。其Attention模块具有时变性和非线性特征，而FFN层被视为知识存储的关键位置。从时间序列角度看，Transformer的输入输出序列符合Granger因果推断的定义，印证了大模型通过预测下一个Token实现类人因果推理能力的观点。模型可通过修改Attention机制或FFN层结构进行优化，例如采用线性化简化（如Mamba）或引入现代连续Hopfield网络。

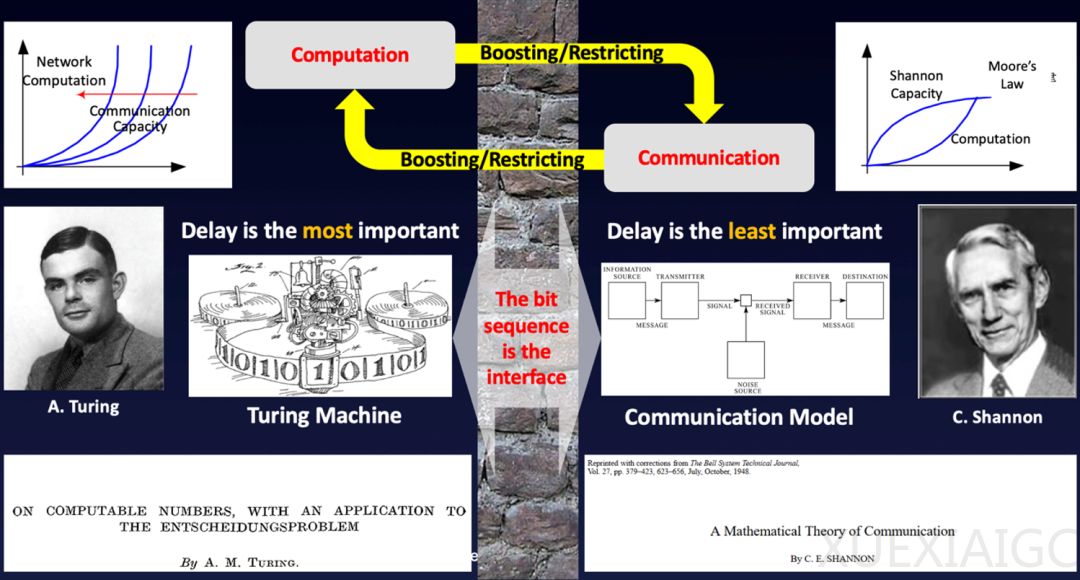
信号处理与信息论的关系在大模型背景下得到新的诠释。信息论关注信息处理的理论极限，而信号处理则聚焦具体实现方法。传统信息论以BIT为核心，而在AI时代，TOKEN成为连接计算与通信的新桥梁。尽管信息论最初仅解决信息传输的技术问题，但通过将核心概念从BIT转向TOKEN，Shannon信息论仍可解释大模型背后的数学原理，这将在后续信息论专题中深入探讨。